Tag: calculation

The Birthday Paradox

By Anupum Pant

Imagine you meet a random person in the street and ask him/her when is their birthday, there’s a huge chance that the person’s birthday will not be the same as your birthday. In fact, the probability of both your birthdays being on the same day is around 0.27%. Fat chance. At the back of our heads, this is something that is very clear to all of us.

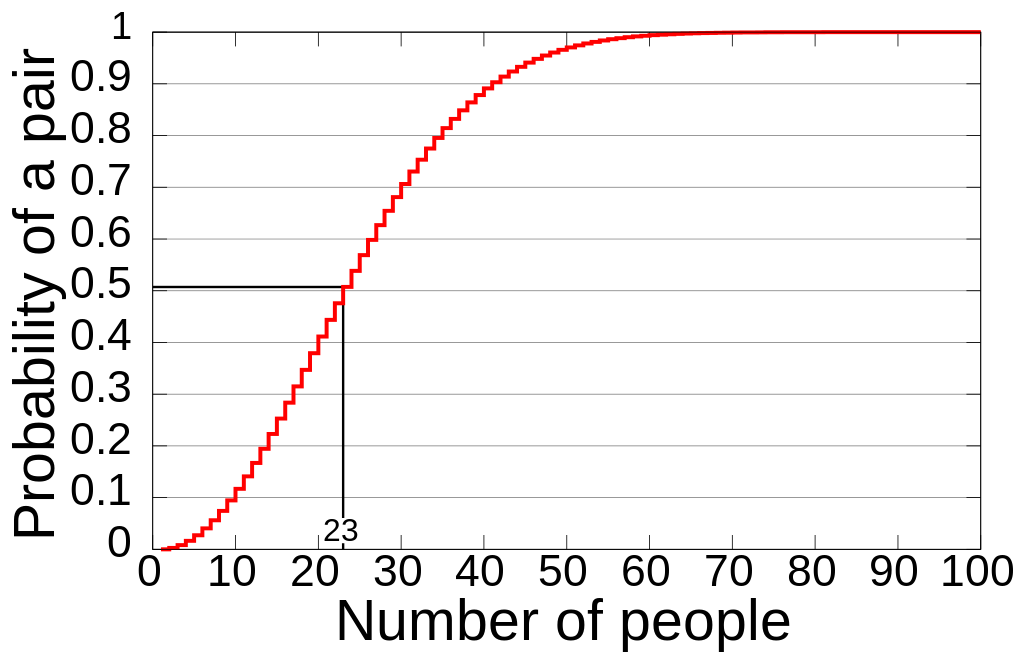
Again, if you repeat this by asking about 22 people the same question, the chance of you finding someone having the same birthday as yours is still around 5%. Too less. This is too is a very intuitive piece of information.

But consider this. If I put all of the 22 guys and you in a room, there’s a big chance that 2 people in that room will have the same birthday – a 50% chance. Moreover, if there are 70 people in the room, this chance increases to about 99.99%. This is called the birthday problem or the birthday paradox.

So, what changed when 20 people went into the room? It was just the fact that in the room, we are picking 2 people from a group of 23 people. That is equivalent to this – everyone is asking everyone their birth dates. Everyone doing it simultaneously makes the probability much higher. The probability of two people sharing a birth date among a group of 23 people is far higher than you alone going around and asking all the 22 people, and finding someone having the same birthday as your’s.

Suppose there are 200 people in the room. The probability of 2 people sharing their birthday is massive (and yet not definite). There is in fact a 99.9999999999999999999999999998% chance!

1024px-Birthday_Paradox.svg

Finally, if you had 367 people in a room, at least a pair among these 367 people in the room would definitely have the same birth date. The 99.99% chance shoots up to a definite (100%) probability if there are 367 people in the same room. Think about it for a minute.

A Piece of Paper as Thick as the Universe

By Anupum Pant

Linear growth is only what we can visualize well. Estimating things that grow exponentially, is something not many of us can do properly.

Here’s what happens when you fold a piece of paper. A paper of thickness 1/10 of a millimetre doubles its thickness. On the second fold it is 4 times the initial thickness and so on. It doesn’t really seem like it would grow a lot after, say, 10 folds, right?

After 10 folds, the paper which was about the thickness of your hair, turns into something that is as thick as your hand.

Without any calculation, how thick do you think would it become if you could fold it 103 times?  (I know, no one has ever folded a paper more than 12 times)

Think about this for a second: How many times do you think would you have to fold a paper to make it 1 kilometre thick? The answer is 23. Yes, it takes just 13 more folds to go from the thickness of a hand to a whole kilometre.

Turns out, if you manage to somehow fold a paper 30 times, it would become 100 km tall. The paper would now reach the space.

For the sake of imagining how exponential growth works, a paper folded 103 times would be about 93 Billion light years thick – which is also the estimated size of the observable universe.

Watch the video below to see one other great example of how exponential growth can mess with you.

Crickets – Nature’s Weather Reporters

By Anupum Pant

Background

An annoying Cricket’s treet-treet-treet noise is really unbearable sometimes, especially when a house cricket ends up under your bed and treets all night long. To others, it’s pleasing, they associate it with the night time, and it makes them go to sleep.

Whatever it is for you, there’s one interesting thing universal about that noise they make. If you can count the number of chirps, you can almost accurately estimate the atmospheric temperature using a simple formula! Good ‘ol farmers used to do this.

I know all of us have smartphones these days, so counting cricket chirps to estimate temperature probably makes no sense to you. Still, I’ve said it back then and I say it again, it’s never bad to know anything.

Here’s how you do it

For doing it, you somehow should be able to measure 14 seconds. In those 14 seconds, count the number of times a single cricket chirps. Suppose there are 35 chirps heard, you save that number and add it to 40 (always 40). And this gives you the present temperature in Fahrenheit.

35 chirps + 40 = 75 degrees Fahrenheit

Now, since only a handful of countries use Fahrenheit to measure temperature, you might want to convert it into Celsius scale. I personally am comfortable with only the Celsius scale. But you don’t have to go through the trouble of converting because, to measure the temperature in Celsius scale using the cricket’s treet, this is what you have to do.

Simply count the number of chirps it makes in 25 seconds. Now divide the number by 3 and add 4 to it. There you have your ambient temperature in Celsius scale. Suppose the cricket chirps 50 times…

(50 chirps/3) + 4 = 20.67 degrees Celsius 

Why it works

To know that it is first important to understand how a cricket makes that sound. Remember only male crickets of a few species make this sound. They do this by a process called stridulation – rubbing 2 body parts to make a sound. Rubbing the underside of one wing with the upper side of the other wing does this trick – as they have rough and hard structures over there.

To move these wings it requires a particular chemical reaction to happen in their muscles. The speed of this chemical reaction is dependent on how hot or cold it is. The hotter it is, the faster the reaction happens and the faster it is able to move its muscles to produce more sounds in those 14/25 seconds…

via [Scientific American] and  [Howstuffworks] and [Farmer’s Almanac]

The Potato Puzzle

By Anupum Pant

Some call it the Potato paradox, but I prefer calling it a puzzle. It isn’t really a paradox. It’s just that we tend to get confused easily when working with such problems and most times end up with the wrong answer. Here’s the question:

You have 100 kg of potatoes. Assume that they are made up of 99% water. Now, you keep them outside to dry for a while. When measured for water content now, they contain 98% water. What do you think is the weight of these dried potatoes now?

Answer quickly first. Then, try and calculate. It isn’t really tough.

Take 15 minutes, or more if you have to. Use papers, pens and calculators if you have to. But whatever you do, stay honest. Don’t search for the solution on the internet, or don’t read further if you haven’t done it yet. Trust me, your brain won’t like the answer.

Solution – [Wikipedia]

The answer is: 50 kg.

For the explanation, watch this visual explanation…

A Mathematical Guide to Optimize Pizza Buying

By Anupum Pant

The logical engineer in me has always paid a lot of attention to how well my money is being put to use, or if something I bought was well worth it. So, before buying anything, I usually love to add in a basic mathematical calculation that would ensure the best logical use of my money. I used to do the same when I was studying engineering and had come up with a handful of tricks, which enabled me to eat the best food, in best quantities at the lowest prices.

Optimized Pizza Buying

Till date, I had relied on calculations for individual joints to buy the pizza that gave me the best value for money (irrespective of what my stomach could fit). In other words, I had never used statistical methods, as I always went to only 2 or 3 pizza places and never felt a need to do it statistically.

So yesterday, while skimming through blogs on NPR, I came across a post by Quoctrun Bui, where he had calculated the best valued pizza size using statistical methods. 

The final findings of his study based on 74,476 prices from 3,678 pizza places were condensed into a graph which depicted data as follows (here is the link to the article for an interactive version of the graph).

pizza guide

Conclusion

The above graph plots 74,476 data points to find the pizza size that gives you the best value for money. The y-axis plots price-per-square-inch – the lesser price-per-square-inch you pay, the better deal you score.

This basically means that buying the largest pizza gets the most value out of your money. As the size increases the value for money increases or the price you pay per-square-inch of pizza decreases. – Statistically speaking.

Adding value

I felt a need to add value to the study by finding how well ‘buying a large pizza’ to get the best value works in India.  So, I selected a popular joint Dominos (where I go all the time) for the test. I dug out their menu (probably an old one) to see if buying the large pizza always works in India. Here is a record of price you pay per square inch at Dominos for various sizes and categories of pizzas. (Click the image to see a better version)

pizza buying guide dominos
I did not pay much attention. Please point if there is a mistake.

Conclusion (Dominos India)

  • No, always buying the large pizza clearly is not the best option at Dominos in India.
  • A small pizza is the best option (economically) if you are buying from the categories: Simply veg, Veg I or Simply Non-veg.
  • A large pizza is the best option (economically) if you are buying from the categories: Veg II, Non-Veg I or Non-Veg II
  • Never go for the small Non-veg II pizza. It is the worst choice you can make.
  • Never ever get a medium pizza from any category!

I’d love to see someone doing the same thing for other popular pizza joints. Do get back to me if you have done it. I’ll add it to the article as an update.

Related articles

 

Enhanced by Zemanta

Gompertz Law – The Dreadful Law of Death

By Anupum Pant

There is no astrologer in the world that can tell you for sure if you’ll die this year or not. But, thanks to Gompertz Law, if you ask me, there is one thing I can tell you for sure – Whatever may be the odds of you dying this year, in 8 years, the likelihood of you dying will double.

This dreadful law of death was named after the first person who noted it – Benjamin Gompertz, in the year 1825. The law rests on a general assumption that a person’s resistance to death decreases as he ages. The Gompertz Law of mortality, put simply in a sentence would compute to this:

Your probability of dying during a given year doubles every 8 years.

It is amazing, and no one knows how it works exactly. Why does nature pick the number 8, to double our likelihood of death? We’ll probably never know.

There is a whole table which relies on census data, and statistically notes the probabilities of people dying at different ages. And when it is plotted on a Probability of death vs. Age graph, you get an exponentially increasing mortality rate with age. That is death coming faster as you get older.

Gompertz Law can be verified for real-life data – the 2005 US census data. The following graph and the probability vs. age plotted using the law match almost perfectly. Amazingly, the law holds true for several other countries too.

gompertz law graph

That means, the probability of me, a 25-year-old dying during the next year is very small — about 1 in 3,000. When I become 33, this probability will grow to something around 1 in 1,500. In the next 8 years, the probability of me dying will be 1 in 750, and so on…At the age 100, the probability a person’s death will be about 1 out of 2 – fat chance of successfully moving on to 101!

Theoretically, using this data, it can be said with 99.999999% certainty that no human will ever live to the age of 130 (of course only if medicine doesn’t start tampering with human genes, or some other artificial factor). There is one thing for sure – there is almost no chance that you are going to beat Mr. Ming.

If you liked this article, do subscribe to my daily newsletter to receive the full articles in your mail everyday. What could be better way to make sure that you learn at least one new thing everyday.