By Anupum Pant
Benford’s law is a fairly simple law to grasp and it will blow your mind. It deals with the leading digits of numbers.
So, for example, you have the number 28 – The leading digit for it would be 2. Similarly, the leading digit for 934 would be 9. Just pick the first digit. Now…
In a data set you’d say – it is common sense to assume that the probability of leading digit one (1) appearing would be more or less equal to that of leading digit nine (9).
As there are 9 possible leading digits, you’d think that the probability of each leading digit would compute to something around 0.11
You’d imagine that it would be normal to assume a nearly straight graph of probability vs. leading digit. But this isn’t true.
Benford’s law says
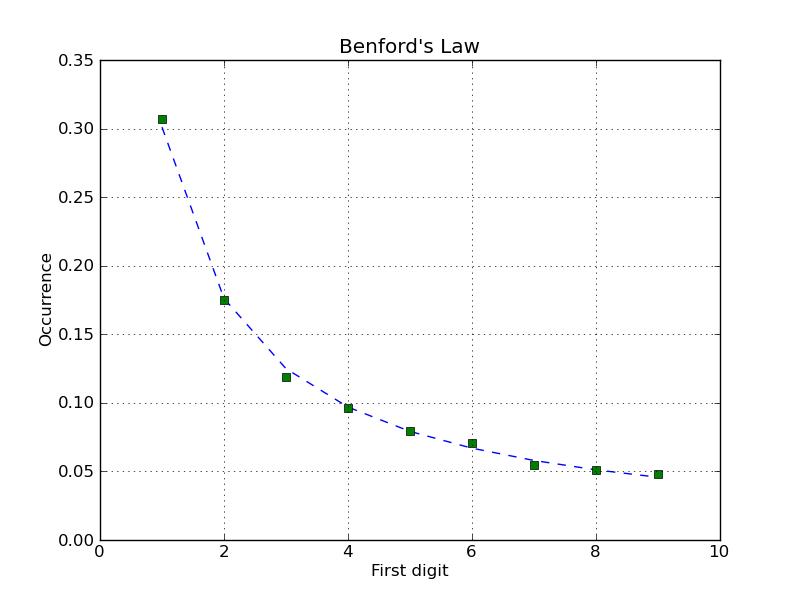
Your common sense fails. What actually happens is that the likelihood of 1 appearing as the first digit in a data set is around 0.3
For the following digits, the probability keeps decreasing. And the following graph appears. You’ll see that the numbers rarely start with nine!
When does it work?
This counter-intuitive result applies to a wide variety of natural data sets. It works the best if your set spans quite a few orders of magnitude. Natural set of data like stock prices, electricity bills, populations, which could range from few single digit values to several digits work the best. Other data like the heights of people doesn’t work because it does not span “quite a few orders of magnitude”. Also, artificially tampered data fails to comply because the person who tampers does the same mistake everyone does. Therefore, Benford’s law is also used to detect frauds in data.
Example:
- Count the number of data points in a data set which have the leading digit 1 and write the number next to the number 1 in a table.
- Then, keep repeating it for all the numbers 2, 3, 4 and so on.
- Calculate the probabilities for each. In the end you’ll be left with a table that would look something like this. (Probability = Number of Data Points for that digit / Total Data Points)
| Leading Digit | Digit Probability |
| 1 | 0.301 |
| 2 | 0.17 |
| 3 | 0.125 |
| 4 | 0.097 |
| 5 | 0.079 |
| 6 | 0.067 |
| 7 | 0.058 |
| 8 | 0.051 |
| 9 | 0.046 |
How does it work?
Watch the following video for the explanation:
Try it yourself: [Kirix]