Tag: math

Mastering The Best Useless Skill – Reading Text in Binary

By Anupum Pant

The next time you see a series of 0s and 1s, you will no longer need to take it to a computer and feed it in to read it. Of course you might never have to read a text in binary, and that is the reason this might be the most useless skill you could master right away. I’m doing it anyway.

Tom Scott from YouTube  recently posted a video on YouTube where he teaches you how to read text written in binary. It’s fairly easy. The only thing you need to practice, if you don’t already know it, is the number that is associated with each alphabet (Like it’s 1 for A and 2 for B and so on).

via [ScienceDump]

Wilson Primes

By Anupum Pant

Thanks to the guys at Numberphile for introducing me to Wilson primes. Although the piece of information that describes Wilson primes itself has more or less no practical use, I still think it’s a good thing to know.

The first thing you need to know is that all prime numbers follow this rule – If you take a prime number P and put it in the following equation you get a number that is perfectly divisible by the prime number P.

The equation: (P − 1)! + 1 = Q

Note: ! is a sign used for factorial. That means P! is equal to the product of all natural numbers smaller or equal to P. So, for example, 3! = 3 X 2 X 1

This rule is valid for all prime numbers and no composite numbers follow it. So, for instance, if you take a composite number for P, the number you get after you put it in the above equation is never divisible by the number itself. This is called the Wilson’s theorem.

Wilson primes (P) are a few special numbers which can divide Q in the equation above two times. So, for example, since 5 is a Wilson prime, you get 25 if you put it in the equation above. And 25 can be divided perfectly by 5 once, and the result (quotient 5) can be divided again by 5 to get a whole number.

Now, for Wilson primes here’s the deal – 5, 13 and 563 are Wilson Primes. And a very interesting thing to note here is that, in spite of all the computing technology we have in the world, these are the only three Wilson primes we know yet.

Mathematicians are pretty certain that there are several other Wilson primes waiting to get discovered, probably infinitely many. But one thing is for sure, below the number 20,000,000,000,000 5. 13 and 563 are the only three which exist.

A Piece of Paper as Thick as the Universe

By Anupum Pant

Linear growth is only what we can visualize well. Estimating things that grow exponentially, is something not many of us can do properly.

Here’s what happens when you fold a piece of paper. A paper of thickness 1/10 of a millimetre doubles its thickness. On the second fold it is 4 times the initial thickness and so on. It doesn’t really seem like it would grow a lot after, say, 10 folds, right?

After 10 folds, the paper which was about the thickness of your hair, turns into something that is as thick as your hand.

Without any calculation, how thick do you think would it become if you could fold it 103 times?  (I know, no one has ever folded a paper more than 12 times)

Think about this for a second: How many times do you think would you have to fold a paper to make it 1 kilometre thick? The answer is 23. Yes, it takes just 13 more folds to go from the thickness of a hand to a whole kilometre.

Turns out, if you manage to somehow fold a paper 30 times, it would become 100 km tall. The paper would now reach the space.

For the sake of imagining how exponential growth works, a paper folded 103 times would be about 93 Billion light years thick – which is also the estimated size of the observable universe.

Watch the video below to see one other great example of how exponential growth can mess with you.

Cutting a Round Cake on Scientific Principles

By Anupum Pant

Background

For years the phrase “cake cutting” has conjured up just one image in my brain – A triangular section of the cake. This way of cutting a cake is so normal that even the tools (especially the spatula) that are made for cake cutting are made in a way that’d work with best when you are making that traditional triangular cut. Turns out, this method of cutting a cake which we’ve all know for years is totally wrong.

Why is it wrong?

It’s wrong mostly for mathematical loners. People who, on their birthday, have no one around to share the cake with, and cannot finish off the whole cake. For them and the ones who have to store the cake after cutting it, are extremely careful about how moist the edges remain when they next eat it, this right way to cut a cake might be of great importance.

The way we’ve always know is “wrong” because when you cut off, say a single section of the cake and decide to store the larger piece in the fridge, some internal part of the cake remains exposed and it dries off. So, the next time you cut off a piece near the area where you started, you’d get a freshly cut moist wall of cake on one side, and a repulsively hard dried up wall on the other. That, some think, is extremely unpleasant.

What’s the Right way?

About 100 years back, a brilliant Polymmath (and a mathematician), Sir Francis Galton, faced a similar annoyance. So, instead of cursing others for having invented an absurdly inefficient way to cut a cake, he decided to develop his own. He ended up developing a very simple and efficient cut which helped him keep the cake wall relatively moist. Here’s how the cut works. (Cut along the dotted line)

the right way to cut a cake

Describing his new way of cutting cakes, he got an article published in the Nature magazine (dated December 20th, 1906). “Cutting a Round Cake on Scientific Principles”

Alex Bellos from the Numberphiles describes it in a video below:

Six Weeks and Ten Factorial – Bizarre Math Coincidence

By Anupum Pant

The number of seconds in 6 weeks might be of little importance to anyone. However there is an interesting bit of trivia related to it, or call it a bizarre mathematical coincidence. Here it is…

The number of seconds in 6 weeks, or 42 days (The answer to life universe and everything) equates to:
6 X 7 (days) X 24 (hours) X 60 (minutes) X 60 (seconds) = 3,628,800 sec
The number 362,880, on the first glance, looks like very random number. Now here is what this number is equal to…

10 factorial (denoted by 10!).
Or simply, 10 X 9 X 8 X 7 X 6 X 5 X 4 X 3 X 2 X 1 = 3,628,800

Down to a single second, the number of seconds in 6 weeks is exactly equal to the numerical 10! Very strange!

One thing you could do is split the 6 weeks calculation into factors, and see it for yourself. The result is all numbers from 1 – 10. The most amazing factoring I’ve ever seen.

If you are too lazy to calculate it yourself, go to this WolframAlpha calculation and see it for yourself. It subtracts 10! seconds from 6 weeks (the result is exactly 0). Apples and Oranges, I know, but the 6 weeks refers to seconds in 6 weeks, here.

6-weeks-and-10-factorial

Salutes to the person who discovered this.

First seen on [Reddit]

The Potato Puzzle

By Anupum Pant

Some call it the Potato paradox, but I prefer calling it a puzzle. It isn’t really a paradox. It’s just that we tend to get confused easily when working with such problems and most times end up with the wrong answer. Here’s the question:

You have 100 kg of potatoes. Assume that they are made up of 99% water. Now, you keep them outside to dry for a while. When measured for water content now, they contain 98% water. What do you think is the weight of these dried potatoes now?

Answer quickly first. Then, try and calculate. It isn’t really tough.

Take 15 minutes, or more if you have to. Use papers, pens and calculators if you have to. But whatever you do, stay honest. Don’t search for the solution on the internet, or don’t read further if you haven’t done it yet. Trust me, your brain won’t like the answer.

Solution – [Wikipedia]

The answer is: 50 kg.

For the explanation, watch this visual explanation…

A Mathematical Guide to Optimize Pizza Buying

By Anupum Pant

The logical engineer in me has always paid a lot of attention to how well my money is being put to use, or if something I bought was well worth it. So, before buying anything, I usually love to add in a basic mathematical calculation that would ensure the best logical use of my money. I used to do the same when I was studying engineering and had come up with a handful of tricks, which enabled me to eat the best food, in best quantities at the lowest prices.

Optimized Pizza Buying

Till date, I had relied on calculations for individual joints to buy the pizza that gave me the best value for money (irrespective of what my stomach could fit). In other words, I had never used statistical methods, as I always went to only 2 or 3 pizza places and never felt a need to do it statistically.

So yesterday, while skimming through blogs on NPR, I came across a post by Quoctrun Bui, where he had calculated the best valued pizza size using statistical methods. 

The final findings of his study based on 74,476 prices from 3,678 pizza places were condensed into a graph which depicted data as follows (here is the link to the article for an interactive version of the graph).

pizza guide

Conclusion

The above graph plots 74,476 data points to find the pizza size that gives you the best value for money. The y-axis plots price-per-square-inch – the lesser price-per-square-inch you pay, the better deal you score.

This basically means that buying the largest pizza gets the most value out of your money. As the size increases the value for money increases or the price you pay per-square-inch of pizza decreases. – Statistically speaking.

Adding value

I felt a need to add value to the study by finding how well ‘buying a large pizza’ to get the best value works in India.  So, I selected a popular joint Dominos (where I go all the time) for the test. I dug out their menu (probably an old one) to see if buying the large pizza always works in India. Here is a record of price you pay per square inch at Dominos for various sizes and categories of pizzas. (Click the image to see a better version)

pizza buying guide dominos
I did not pay much attention. Please point if there is a mistake.

Conclusion (Dominos India)

  • No, always buying the large pizza clearly is not the best option at Dominos in India.
  • A small pizza is the best option (economically) if you are buying from the categories: Simply veg, Veg I or Simply Non-veg.
  • A large pizza is the best option (economically) if you are buying from the categories: Veg II, Non-Veg I or Non-Veg II
  • Never go for the small Non-veg II pizza. It is the worst choice you can make.
  • Never ever get a medium pizza from any category!

I’d love to see someone doing the same thing for other popular pizza joints. Do get back to me if you have done it. I’ll add it to the article as an update.

Related articles

 

Enhanced by Zemanta

Gompertz Law – The Dreadful Law of Death

By Anupum Pant

There is no astrologer in the world that can tell you for sure if you’ll die this year or not. But, thanks to Gompertz Law, if you ask me, there is one thing I can tell you for sure – Whatever may be the odds of you dying this year, in 8 years, the likelihood of you dying will double.

This dreadful law of death was named after the first person who noted it – Benjamin Gompertz, in the year 1825. The law rests on a general assumption that a person’s resistance to death decreases as he ages. The Gompertz Law of mortality, put simply in a sentence would compute to this:

Your probability of dying during a given year doubles every 8 years.

It is amazing, and no one knows how it works exactly. Why does nature pick the number 8, to double our likelihood of death? We’ll probably never know.

There is a whole table which relies on census data, and statistically notes the probabilities of people dying at different ages. And when it is plotted on a Probability of death vs. Age graph, you get an exponentially increasing mortality rate with age. That is death coming faster as you get older.

Gompertz Law can be verified for real-life data – the 2005 US census data. The following graph and the probability vs. age plotted using the law match almost perfectly. Amazingly, the law holds true for several other countries too.

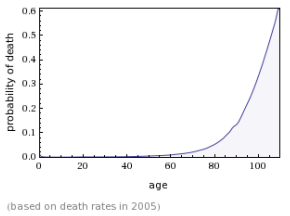
gompertz law graph

That means, the probability of me, a 25-year-old dying during the next year is very small — about 1 in 3,000. When I become 33, this probability will grow to something around 1 in 1,500. In the next 8 years, the probability of me dying will be 1 in 750, and so on…At the age 100, the probability a person’s death will be about 1 out of 2 – fat chance of successfully moving on to 101!

Theoretically, using this data, it can be said with 99.999999% certainty that no human will ever live to the age of 130 (of course only if medicine doesn’t start tampering with human genes, or some other artificial factor). There is one thing for sure – there is almost no chance that you are going to beat Mr. Ming.

If you liked this article, do subscribe to my daily newsletter to receive the full articles in your mail everyday. What could be better way to make sure that you learn at least one new thing everyday.

Klein Bottle – A Bottle That Contains Itself

By Anupum Pant

To appreciate the beauty of mathematics and nature there is no escaping without learning about a Klein Bottle. A three-dimensional representation of a Klein bottle looks like this – [image]

There are number of phrases you can use to describe (not exhaustively) it. A few of them are as follows:

  • An object with no boundaries.
  • An object with no inside or outside.
  • One sided surface.
  • Non-orientable surface

Wikipedia describes it as:

The Klein bottle is a non-orientable surface; informally, it is a surface in which notions of left and right cannot be consistently defined.

Simplifying things: A Möbius strip is a simpler example of a non-orientable object. That means it has no inside or outside. Add another aspect – having no boundaries – to it, it gets more complex and you end up with a Klein bottle.
If you haven’t heard of Möbius strips, to understand such surfaces, you can make one for yourself now.

  1. Tear off a strip of paper.
  2. Hold it horizontally, straight with both of the short edges in your hands.
  3. Now, twist one of the edges by 180 degrees and join the two short edges. You’ll have something like this in your hands – [image]

Test the surface and edges: On this object you just created, move your finger along the surface. You’ll find that your finger comes  back to the same place eventually. There is no inside or outside for this object, there is just one surface.
The same thing happens with its edge (try moving your finger along the edge). Here is a Music box playing a Harry Potter theme continuous – forward, inverted, forward and so on – manner; Relevant video: [video]

Now spin it (the Möbius Strip) fast. You can NOT practically do it. I mean, spinning it like you spin a circle and get a sphere. There! You have a Klein bottle. It is better than a Möbius strip in a way that it (Klein Bottle) has no boundaries.

Klein bottles cannot actually exist in our three-dimensional worlds, the ones that look like them (Klein Bottles) are just 3D representations of a 4D object. Like a two-dimensional drawing of a 3D cube. These models are available for you to buy. Interestingly, in spite of having no inside or outside, they can be filled with a liquid. But, given the opposing force of air, they are pretty tough to fill. It is important to note that the 3D representation of a 4D Klein bottle has an intersection of material, this doesn’t happen in 4D. It is like the intersecting edges of a 3D cube in the 2D representation.

You’re thinking 3D? At MIT (and other places) 4D printing is already happening.

If you are having a tough time imagining this 4D object, the following 4D animation might help (or leave you perplexed) – [video]
[Extra reading for math geeks] as if they already didn’t know about Klein bottles.