Tag: maths

The Number of the Beast

By Anupum Pant

666 is probably one of the most infamous numbers and is known by many as the number of the beast. That is because the Bible, as translated in English, mentions 666 as the number of the beast. Revelation 13:18 says this…

Let the one who has understanding calculate the number of the beast, for it is the number of a man, and his number is 666.

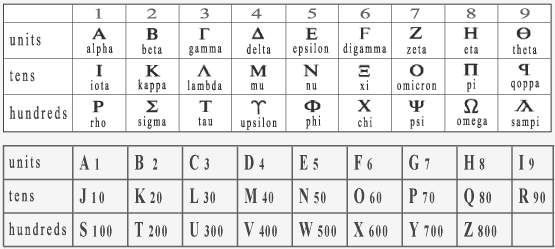
However, it is very interesting to note that, since the Bible wasn’t written originally in English, the number 666 wasn’t actually there in the original form. In the original Greek manuscript, a language (like Hebrew) which uses letters for numbers, the number is written as 3 letters. I did not know this before. That means, all of the Greek and Hebrew text can also be read as numbers!

This is called isosephy – Meaning a practice of writing text where a text can be a number too. Normally the number values associated with each letter of a word are added to form a number.

So, the letters of my name (A, N, U, P, U, M), in order, would be the numbers: 1, 50, 300, 70, 300, 40. Total: 761 – Which is not very close to 666, I’m not a beast. What about yours? You can look at the table below and calculate.

Nero Caesar written in Hebrew can be converted to numbers and the total is 666. A way of saying, by the author, that Nero Caesar is the root of all evil. At the same time, the author doesn’t end up in trouble for writing this.

ris5en

 

Also, all the 36 numbers on a Monte Carlo roulette wheel add up to 666. Watch more in the video below.

The Birthday Paradox

By Anupum Pant

Imagine you meet a random person in the street and ask him/her when is their birthday, there’s a huge chance that the person’s birthday will not be the same as your birthday. In fact, the probability of both your birthdays being on the same day is around 0.27%. Fat chance. At the back of our heads, this is something that is very clear to all of us.

Again, if you repeat this by asking about 22 people the same question, the chance of you finding someone having the same birthday as yours is still around 5%. Too less. This is too is a very intuitive piece of information.

But consider this. If I put all of the 22 guys and you in a room, there’s a big chance that 2 people in that room will have the same birthday – a 50% chance. Moreover, if there are 70 people in the room, this chance increases to about 99.99%. This is called the birthday problem or the birthday paradox.

So, what changed when 20 people went into the room? It was just the fact that in the room, we are picking 2 people from a group of 23 people. That is equivalent to this – everyone is asking everyone their birth dates. Everyone doing it simultaneously makes the probability much higher. The probability of two people sharing a birth date among a group of 23 people is far higher than you alone going around and asking all the 22 people, and finding someone having the same birthday as your’s.

Suppose there are 200 people in the room. The probability of 2 people sharing their birthday is massive (and yet not definite). There is in fact a 99.9999999999999999999999999998% chance!

1024px-Birthday_Paradox.svg

Finally, if you had 367 people in a room, at least a pair among these 367 people in the room would definitely have the same birth date. The 99.99% chance shoots up to a definite (100%) probability if there are 367 people in the same room. Think about it for a minute.

An Elegant Proof of the Pythagorean Theorem by a Former US President

By Anupum Pant

Abraham Lincoln, the 16th president of the United States, was probably a math whiz. Doesn’t it sound like an extremely rare combination of things a person could possibly be? – a president and a math whiz. And yet, he was not the only one. James Garfield, the 20th president, was very much into mathematics too.

Garfield wasn’t a professional mathematician. He was a president. But, much like Abraham Lincoln, he was very much into geometry! Before he went into politics, he wanted to become a mathematics professor.

While he was a member of the US house of representatives, five years before he was elected president of the US, he came out with a very elegant and unique proof of the Pythagorean theorem (yes, another one of those Pythagorean theorem proofs). Here’s how he did it with the help of a congruent flipped triangle…

Doing it with a piece of paper is really easy…

Pythagorean theorem proofFold a paper and cut 2 exactly same right-angled triangles out of it. Now, put them together as shown in the image here (click the image). Next, write down the area of the trapezium – (a + b) . ½(a + b) – 1

Now write the area of all the 3 triangles and add them. This is what you’d get – 2 x ½ ab + ½ c2  – 2

Since both these areas are same, just written in a different way, equate them and solve. You’ll end up with the Pythagorean theorem!

a2 + b2 = c2 

Or, simply watch the video to understand better…

Unsolvable Problems – A Math Story With a Moral

By Anupum Pant

True Story

Back in 1939, a first year doctoral student at Berkeley, George Dantzig arrived late for a statistics class one day. On the board, professor Jerzy Neyman, a renowned mathematician, had written two problems, and it wasn’t very clear to George what he had written them were for. As any other student would assume, George assumed them to be homework problems and noted them down.

He went back and started working really hard on those problems. They seemed a little harder than usual to him. Nevertheless, George was determined enough. After a couple of days, when George was satisfied with his solution, he went to his professor and apologized to him for taking so long to finish the homework. Without looking at what he had done, the professor told him to put the work on his table, and he’d see it later. George did exactly that.

Six weeks later, on an unsuspecting Sunday morning, at 8:00 in the morning, George was awakened by a frantic knock on the door. It was professor Neyman. With a pile of papers in his hands, he seemed very excited. It was only then, through professor Neyman, that George came to know what he had done on those papers six weeks back.

Six weeks back, those two problems which George mistook for homework turned out to be two examples of unsolved statistics problems Neyman had written on the board. George had unknowingly noted them as homework, and ended up solving the 2 unsolved statistics problems.

Later the papers on these problems were published. However the second one was published much later, in the year 1950.

Moral: When people are not tied down by prejudice, by putting in good work, they often manage to achieve extraordinary things.

Via [Snopes]

The New York Pizza and Subway Ride Connection

By Anupum Pant

This is funny and interestingly true at the same time. According to Eric M. Bram of New York, there’s an unspoken rough law that says – there’s a connection between the price trends of a pizza* and a subway ride ticket in the New York city.

Their prices have remained more or less same for about 50 years now, moving up and down together! If one goes up, the other has been seen to move in the same direction too. The trend has been observed to be more or less valid for the last half century. 

Don’t ask why. I say, just go with the flow.

It was first observed in the year 1980 by Eric M. Bram. He observed that there was an uncanny similarity in the price of a slice of a pizza and a subway token in the year 1960, in the NYC – Both 15 cents.

In the 70s pizza started costing about 35 cents. So did the subway token! and so on…

Fairly recently, in the year 2002, when the price of pizza was about $2.00, and the price of a subway token was $1.50, it was predicted that the price of the subway ticket would rise. And as the “law” states, it did!

Again in the year 2005, the price of pizza went up to $2.25 and it was predicted that the subway token price would rise. It did again!

Once again in the year 2007. In 2013 the fare moved to $2.50, again just after the average pizza price had risen to the same price. No one probably knows why.

With 50 years of record, I’m pretty sure that the trend is going to keep up. Some one from the future, living in New York could confirm it in the comments section below.

So, if someone starts mass producing pizzas, floods the pizza market in the NYC, and drops the price, will the Subway ticket drop too? Someone should try that. 

*When we say pizza here, specifically, we are talking about a plain tomato + mozarella + crust pizza only.

A Fun Way to Multiply Numbers

By Anupum Pant

Please note, in the heading I said, a fun way to multiply numbers, not necessarily a quick way. Widely touted as an “amazingly quick Japanese method to multiply”, I think firstly, it really is not a very quick method. Secondly, I couldn’t find any sources confirming that it is a method developed by the Japanese. In fact, I’m not even sure if there’s anything Japanese about it. Nevertheless, the method sure is fun and should work great for people who don’t remember the multiplication tables well.

Another great thing about it is that it is a multiplication problem turned into a visual counting  problem. Since multiplication exercises don’t really make kids happy, they’d definitely love to count intersections instead (multiplication disguised intelligently).

Of course the counting can be used for single digit numbers too, but that won’t be too useful. For slightly more complex problems involving 2 digits like 32 X 42, it could be a life saver. It’s a fairly simple 3-step process. Here’s how you do 32 X 42 with it…

Step 1Step 1: The best way to go about it is by starting from the top left. First, you draw the 3 lines for the 3 of the number 32. And then you make 2 lines for the number 2, as shown.

Step 2

Step 2: Next make 4 lines and 2 lines intersecting the previously made lines as shown. Clearly, 4 lines for the 4 of 42 and 2 lines for the units place of 42.Step 3

 Step 3: Count the number of intersections in the far left (a), centre (b), and the far right (c). (a), (b) and (c) are 12, 14 and 4 respectively, for this problem.

The 1 from 14 gets carried to the number just at the right of it – 12 of (a), and (a) becomes 13. A similar carrying of the ten’s place to the immediate right column happens if there are any 2 digit numbers. So you are left with 13, 4 and 4 now. 1344 is the answer to 32 X 42.

This can be done for 3 digits too and more…
If there’s a zero, you could make a line and not count any intersections with it. As it has been shown in the video below…

Please hit like if you learnt something from this article.

The Potato Puzzle

By Anupum Pant

Some call it the Potato paradox, but I prefer calling it a puzzle. It isn’t really a paradox. It’s just that we tend to get confused easily when working with such problems and most times end up with the wrong answer. Here’s the question:

You have 100 kg of potatoes. Assume that they are made up of 99% water. Now, you keep them outside to dry for a while. When measured for water content now, they contain 98% water. What do you think is the weight of these dried potatoes now?

Answer quickly first. Then, try and calculate. It isn’t really tough.

Take 15 minutes, or more if you have to. Use papers, pens and calculators if you have to. But whatever you do, stay honest. Don’t search for the solution on the internet, or don’t read further if you haven’t done it yet. Trust me, your brain won’t like the answer.

Solution – [Wikipedia]

The answer is: 50 kg.

For the explanation, watch this visual explanation…

A Thread Around the Earth

By Anupum Pant

Background

Couple of days back, I read about a puzzling geometrical conundrum, probably on Quora. It might not sound amusing to you math geeks out there, but to me, it sounded like an impossible thing at first. The sad part is, I did not save the source link in my notes. Thankfully, I did care to note down the idea. Let me call it the “Thread wound Around the Earth” puzzle.

Here is a simple question first. Try answering it without any calculation. Just guess. Be honest to yourself, don’t see the answer just below it. Scroll slow.

As BBC’s website puts it…

Imagine a piece of string wrapped around the Earth’s equator – that’s about 40,000km. How much MORE string would you need for it to sit 15cm above the ground, all the way around?

A) 1 metre, B) 1 kilometre or C) 1,000 kilometres

Thread wound around the Earth

The answer is A) 1 meter. Yes, just 1 meter of extra rope.

Suppose, you have an outrageously long thread with you. You tie it around the base of a tree, somewhere at the equator. Now, you go around the earth, along the equator, carrying the thread with you, till you come back to that tree where you started. At this point, you’ll have a thread that goes around the earth in a circle. At every point, let us imagine that the rope is taut and touching the ground (there are no mountains or valleys in between). It’s a perfect circle (assume).

Suppose, you still have an extra meter of the rope left now. So, you break the wound rope at one point and add the extra meter to it. That of course slackens the wound rope. For this rope to be taut again, it has to be lifted up by some amount. What do you think that distance would be from the ground? Assume that the rope still makes a huge circle just above the ground and lifts by equal amount at every point along the equator.

Just the extra meter of rope, causes the rope to rise by ~15 cm all around the earth (actually 15.9 cm). For a single meter of rope added to a 40,000 km of rope, that sure seems like a huge lift! But that isn’t all…

rope 15 cm above earth

The most amazing part is that, no matter what the size of the circle, a meter of increased circumference will increase the radius by ~15 cm. Always!

Try tying a rope around a golf ball, or even try doing that around the sun. It’s always that – 1 meter increase in circumference, always increases the radius by ~15 cm.

The Math is so straightforward.

If you think about it mathematically, it is completely straightforward.

Radius X 2 X Pi = Circumference

That means, the Radius is directly proportional to the circumference of a circle. Everyone knows that. So, the amount of change in the radius is reflected proportionally in the circumference, the magnitude of radius can be anything, really. So it’s pretty natural that just a single meter of rope is required to lift the rope by 15.9 cm around any circle. The size doesn’t matter. But practically thinking, the above question makes it seem impossible.

Please hit like if you learnt something from the article.

10 Fancy Units of Measurement

by Anupum Pant

There exist a few unusual units of measurement which you must have never heard of, or would have never thought of them as units until now. Here is a list of 10 of the many fancy units of measurement.

Note: These units are not official. They’re often used for their humor value or for simplicity’s sake):

1. Car length – It is not a very unusual unit of measurement and is used normally to mention the braking distance of a vehicle. Deriving its length from a typical car’s length, 4 meters is referred as one “car length”. You must have heard one spy advising another spy to keep a 2 car length distance from a vehicle to avoid detection.

2. Nanoacres – A measure of area which is equal to about 4 sq.mm (4.0468564224 sq.mm exactly). It is the area of a single VLSI chip which is square in shape and measures 2 mm on each side. This unit is widely popular as a joke among electronic engineers – who often are known to make quips about VLSI nanoacres having costs in the same range as real acres.

3. Grave – It is a unit that measures mass and equals 1 kilogram or 1000 grams. Grave was set to be the standard unit of mass for the metric system, but it was replaced by kilogram in 1799. [read more about it]

4. Moment – Moment is actually something that was used to measure 90 seconds during the Medieval times. But for modern times, the Hebrew calendar’s definition of moment makes more sense. According to it, a moment is equal to 5/114 of a second or around 0.0438  seconds. [read more]

5. Jiffy – Jiffy is used popularly as an informal time in English. Think of someone saying “I’ll be back in a jiffy”. But, we’ve never thought of it as a unit. Also, every field has a different definition of Jiffy.

  • Early usage – 33.35 picoseconds or the time take by light to travel 1 cm.
  • Electronics – 1/50th or 1/60th of a second, depending on the AC power supply frequency.
  • Computing – Typically anything between 1 millisecond to 10 millisecond. Commonly: 10 ms.
  • Animation – The time interval between each frame of a dot GIF file or 1/100th of a second or 10 ms.
  • Physics/Chemistry – Time taken by light to travel 1 Fermi or 3X10^-24 seconds.

6. Dog Year – Based on a popular myth that dog’s age can be calculated in human years by multiplying it with 7. So, a single Dog year comes to around 52 days (365/7 – Days in a human year divided by 7)

7. A Bible – Used as measure of digital data volumes. It is like measuring the size of a disk in number of movies it can fit which I used in this article. A single Bible in uncompressed 8-bits, has around 4.5 million characters and 150 of them can be stored in a single CD. Hence, a bible can be measured to be approximately equal to 4.67 Megabytes. Similarly,  Encyclopedia Britannica and Library of Congress are used to represent much larger data volumes.

8.  Kardashian – Yes, it is named after the 72 day marriage of  Kim Kardashian to Kris Humphries. Of course, it measures 72 days of marriage. So, a 25 year marriage would amount to around 126.7 Kardashians.

9. Wheaton – Used to measure the number of twitter followers relative to the popular celebrity Will Wheaton. This became a standard when he had 0.5 million Twitter followers. Today, Will Wheaton himself has 4.88 Wheatons. I, for instance, with 210 followers, have about 0.00042 Wheatons.

10. Warhol – Derived from the widely used expression coined by Andy Warhol – “15 minutes of fame” – 1 Warhol measures exactly what you’d expect it to – 15 minutes of fame. Yes, it measures the amount of fame.
Consequently, 1 kilowarhol is equal to 15,000 minutes of fame or 10.42 days and 1 megawarhol measures 15 million minutes of fame or about 28.5 years.