Tag: way

Cutting a Round Cake on Scientific Principles

By Anupum Pant

Background

For years the phrase “cake cutting” has conjured up just one image in my brain – A triangular section of the cake. This way of cutting a cake is so normal that even the tools (especially the spatula) that are made for cake cutting are made in a way that’d work with best when you are making that traditional triangular cut. Turns out, this method of cutting a cake which we’ve all know for years is totally wrong.

Why is it wrong?

It’s wrong mostly for mathematical loners. People who, on their birthday, have no one around to share the cake with, and cannot finish off the whole cake. For them and the ones who have to store the cake after cutting it, are extremely careful about how moist the edges remain when they next eat it, this right way to cut a cake might be of great importance.

The way we’ve always know is “wrong” because when you cut off, say a single section of the cake and decide to store the larger piece in the fridge, some internal part of the cake remains exposed and it dries off. So, the next time you cut off a piece near the area where you started, you’d get a freshly cut moist wall of cake on one side, and a repulsively hard dried up wall on the other. That, some think, is extremely unpleasant.

What’s the Right way?

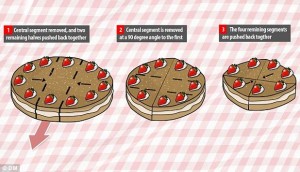
About 100 years back, a brilliant Polymmath (and a mathematician), Sir Francis Galton, faced a similar annoyance. So, instead of cursing others for having invented an absurdly inefficient way to cut a cake, he decided to develop his own. He ended up developing a very simple and efficient cut which helped him keep the cake wall relatively moist. Here’s how the cut works. (Cut along the dotted line)

the right way to cut a cake

Describing his new way of cutting cakes, he got an article published in the Nature magazine (dated December 20th, 1906). “Cutting a Round Cake on Scientific Principles”

Alex Bellos from the Numberphiles describes it in a video below:

A Fun Way to Multiply Numbers

By Anupum Pant

Please note, in the heading I said, a fun way to multiply numbers, not necessarily a quick way. Widely touted as an “amazingly quick Japanese method to multiply”, I think firstly, it really is not a very quick method. Secondly, I couldn’t find any sources confirming that it is a method developed by the Japanese. In fact, I’m not even sure if there’s anything Japanese about it. Nevertheless, the method sure is fun and should work great for people who don’t remember the multiplication tables well.

Another great thing about it is that it is a multiplication problem turned into a visual counting  problem. Since multiplication exercises don’t really make kids happy, they’d definitely love to count intersections instead (multiplication disguised intelligently).

Of course the counting can be used for single digit numbers too, but that won’t be too useful. For slightly more complex problems involving 2 digits like 32 X 42, it could be a life saver. It’s a fairly simple 3-step process. Here’s how you do 32 X 42 with it…

Step 1Step 1: The best way to go about it is by starting from the top left. First, you draw the 3 lines for the 3 of the number 32. And then you make 2 lines for the number 2, as shown.

Step 2

Step 2: Next make 4 lines and 2 lines intersecting the previously made lines as shown. Clearly, 4 lines for the 4 of 42 and 2 lines for the units place of 42.Step 3

 Step 3: Count the number of intersections in the far left (a), centre (b), and the far right (c). (a), (b) and (c) are 12, 14 and 4 respectively, for this problem.

The 1 from 14 gets carried to the number just at the right of it – 12 of (a), and (a) becomes 13. A similar carrying of the ten’s place to the immediate right column happens if there are any 2 digit numbers. So you are left with 13, 4 and 4 now. 1344 is the answer to 32 X 42.

This can be done for 3 digits too and more…
If there’s a zero, you could make a line and not count any intersections with it. As it has been shown in the video below…

Please hit like if you learnt something from this article.