Tag: black

The Langton’s Ant

By Anupum Pant

Think of a cell sized ant sitting on a huge grid of such white cells. The thing to note about this ant is that it follows a certain sets of simple rules. The main rule is that when the ant exits a cell, it inverts the colour of the cell it just left. Besides that:

  1. If the ant enters a white square, it turns left.
  2. If it enters a black square, it turns right.

Here’s what happens if the ant starts out in the middle and moves to the cell on the right, as a starting step (this can be on any side).

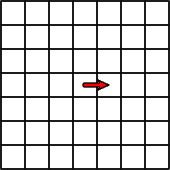
First step, it goes to the right.
First step, it goes to the right.
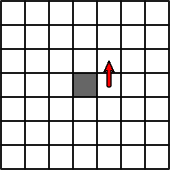
Enters a white cell and rule 1 kicks in. The exited cell is inverted in colour and it turns left.
Enters a white cell and rule 1 kicks in. The exited cell is inverted in colour and it turns left.
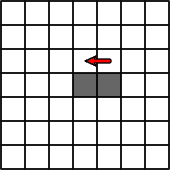
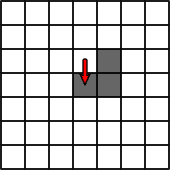
Enters a white cell and rule 1 kicks in. The exited cell is inverted in colour and it turns left. (Again)
Enters a white cell and rule 1 kicks in. The exited cell is inverted in colour and it turns left. (Again)
Enters a white cell and rule 1 kicks in. The exited cell is inverted in colour and it turns left. (Again)
Enters a white cell and rule 1 kicks in. The exited cell is inverted in colour and it turns left. (Again)
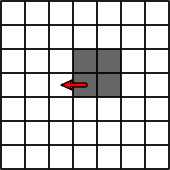
Enters a black cell and rule 2 kicks in. The exited cell is inverted in colour and it turns right.
Enters a black cell and rule 2 kicks in. The exited cell is inverted in colour and it turns right.
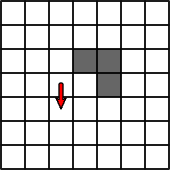
Rule 1 again and so on...
Rule 1 again and so on…

Now as this continues, a seemingly random figure starts taking shape. The black cells are in total chaos, there seems to be no specific order to how they appear on the canvas. (of course the pattern is always the same chaos, considering the ant starts on a blank array of cells).

And yet, after about 10,000 steps are completed by the turing ant, it starts creating a very orderly highway kind of figure on the canvas. It enters an endless loop consisting of 104 steps which keeps repeating for ever and creates a long highway kind of structure.

Suppose, initially you take a configuration of black spots on a canvas (not a blank white canvas). Take an array of cells with randomly arranged black spots, for instance. If given enough time, the ant ultimately always ends up making the looped highway. However, before it starts doing it, it might take a significant amount of steps less, or more, than the ~10,000 steps it took to reach the loop in a blank array of cells.

No exception has ever been found. A computer scientist Chris Langton discovered this in the year 1986.

The Landolt Clock Reaction

By Anupum Pant

Steve Spangler Never ceases to amaze me. Once again I found this old video of him on the Ellen show. These are a few experiments he does on the stage…

  • Lights a tube light with his bare hands and Ellen’s.
  • A transparent liquid suddenly instantly changes colour.
  • Blows the hydrogen and oxygen mixture on Ellen’s hand.
  • And makes someone from the audience walk across the table on a non newtonian fluid.

Steve doesn’t exactly explains what happens there, but the second experiment is my favourite. It is the one in which he asks Ellen to pour two transparent liquids into each other and mix them well. Then Ellen waits for a few seconds and the liquid instantly turns into an ink like colour.

The magical effect is actually a chemical reaction known as the Landolt Clock Reaction. It actually involves 3 different solutions (read about them). The reaction happens quicker once the mixing starts and leads to a third reaction which happens immeasurably fast. It’s totally instantaneous and thus the transparent solutions turn into a bluish black iodine starch complex. As steve’s website puts it…

The sudden change from a colorless solution to the blue-black solution is the result of four sequential reactions. First, the bisulfite ions (HSO3-) reduce some of the iodate ions (IO3-) to form iodide ions (I-). Next, the iodide ions (I-) are oxidized by the remaining iodate ions (IO3-) to form triiodide ions (I3-). The solution now consists of triiodide ions (I3-) and soluble starch. In the third reaction, the triiodide ions (I3-) get reduced by the bisulfite ions (HSO3-) to become iodide ions (I-). That continues until all of the bisulfite has been consumed. Finally, the triiodide ions and starch combine to form the dark blue-black starch complex that looks like ink.

See more at: SteveSpanglerScience

It Sure is Magnetic, But is it Solid or Liquid?

By Anupum Pant

Figuring out if glass is a solid or liquid is pretty straight forward. This putty in the video however, behaves a lot like pitch (the same thing that was used for the world’s longest continuously running experiment). On applying a greater and abrupt impact, it shatters like a ceramic. While it flows like a liquid if you let it. But that is not even the point.

The point is, it can be magnetized! And it sure is another one of those awesome science toys you can have on your desk all the time. By the way, the other ones are Gombocs, constantwidth objects and feel flux. It must so much fun to play around with such a gooey magnetic material (putty). Some good soul will gift it to me for my birthday…may be.

It stretches, bounces, breaks, flows, can be magnetized and what not! It’s like the ferro fluid, but more awesome. Even this, like ferro fluid, has very very tiny magnetic particles dispersed in a putty like substance which makes it magnetic.

Who wouldn’t want to try out that Neodymium magnet swallowing trick! Since it looks like it’s live, they call it the magnetic thinking putty. Perfect name, I must say.

The Sweet Tale of the Mysterious Tree Lobster

By Anupum Pant

I do realize how big our world is and the sheer number of species that live in it. Also the fact that about 86% of the species are still unknown has me in awe all the time.

Yet, after having read about so many kinds of animals that live on our planet, after having documented them on this blog, I always feel that I’ve known and written it all. The very moment I start losing hope that I would never find an interesting animal ever again, something incredible comes across. Always!

Today, that happened again when I was reading an NPR blog. This time, there’s more than the species itself. The place where it lives is pretty awesome too. The most amazing part – This six-legged giant lives only there. That means, nowhere else on Earth will you find it! First, let’s see where it lives…

This is where it lives:

balls pyramid

I know, it looks like a CG mountain done for a fantasy movie. Trust me, it’s real. It’s called the Ball’s Pyramid (named after a European named Ball who first saw it in 1788) and was formed 7 million years ago due to a volcanic eruption. It is an awkwardly tall (1,844 feet) and an extremely narrow rock sitting in the centre of the sea. To the East of Australia, the red place marker in the following picture shows where the rock is located.

balls pyramid location

 What lives there? And how was it found?

There is an island – Lord Howe island – close to the rock. In the island lived huge “tree lobsters” (actually they were huge stick insects with a hard exoskeleton – Dryococelus australis). In the year 1918, a ship crashed on the island and brought with it some rats. The rats loved these tree lobsters and finished them off within 2 years. After 1920, these tree lobsters were thought to be extinct.

tree lobster

Of course there were stories of these insects living on a rock near the island. But no human wanted to climb the narrow rock to hunt insects at night.

Only in the year 2001 when 2 researchers David Priddel and Nicholas Carlile decided to climb up the rock to find out if these stories were real, they found something incredible. Poop of a large insect. When the came back at night to investigate, the shiny black huge tree lobsters were found! These insects had probably never been extinct.

For more than 80 years, 24 of them had been living on this rock, in a bush and no one knew how they got there. Probably they clinged on to birds or something. Also, according to the researchers, these creatures have never been seen anywhere else.

Where are they now

I’m not sure about where they are now. According to the 2012 NPR article which I read, a pair of these creatures – Adam and Eve – were brought into Australia. Eggs got laid and little Tree lobsters came into the world. Thankfully, the species was saved from going extinct. But it isn’t known if they’ll be sent back to their home island because the great-great-great grandsons of those rats must still be there waiting to finish these insects off again.

This is how the first ones hatched in the zoo…

Hit like if you learnt something from this article.

Snow Does Not Melt Like You Think It Would

By Anupum Pant

Background

For the last several days, the national average temperature in the US plunged by a several notches when the country was invaded by the bitingly cold polar vortex winds from the arctic, not once, twice. For the second time, the eastern sea board experienced a lot of trouble. So much that the state of Georgia, Alabama, Mississippi, Louisiana, North Carolina and South Carolina declared a state of emergency. People got trapped for hours, hundreds of accidents were reported and schools had to shut down.

Conspiracy theories

Of course with the extremely cold winds came an abnormal amount of snow. And like always, even the seemingly harmless snow spurred a few theorists to spin out conspiracy theories. There were stories going viral that suggested that the crazy amounts of snow was actually “geo-engineered” and was being sent down by the government, stuffed with nano-bots to control the minds of people.

What backed them? The theories were backed with a claim that the material falling down from the sky was not actually snow and something else which did not melt when held against a flame. Videos showing people trying to melt the snowballs using a cigarette lighter went viral. In fact, the snow as it’d be expected to, wasn’t melting, it was collapsing. Like a Styrofoam dipped in acetone, or Styrofoam held against a flame would do, snow was mysteriously disappearing from around the flame. There was no dripping water. Moreover, the concave part of the snow was left with a black charred mark like plastic would!

Busted!

Turns out the “mysterious material” was nothing more than normal snow. The lesser known fact that snow does not melt like we’d  expect it to, made people believe in the weird theories.

Yes, snow does not melt like normal ice. I mean it does melt, but it leaves almost no dripping water when the rate of melting is slow. Now, why is that?

Since, snow is porous, it contains several little holes that can suck in the water just like a tissue paper with tiny holes is able to soak in water. This particular process soaking, where tiny solid holes suck liquid, is termed as capillary action and is the same action which enables plants to suck in water from the ground and send it to the higher parts without any motor attached.

The soaking in a snowball happens in real-time. As the water gets melted, it gets soaked instantly, there is no time for the water to drip. This explains the collapsing snow.

The “charred snow” is due to the unburnt carbon left from the fuel of the lighter, not because it is made of plastic. Astronomer and science writer Phil Plait explains it in the video below. [Video]

via [PopSci]

Related articles
Enhanced by Zemanta